martes, 14 de junio de 2011
viernes, 20 de mayo de 2011
Polígonos
Polígonos
Los polígonos nacen junto con la geometría, y su origen fue en el antiguo Egipto, donde estas figuras geométricas surgieron con la necesidad de dividir y medir los terrenos destinados a la agricultura.Luego con el avance en el estudio de la geometría realizado por los griegos, los conocimientos sobre los polígonos también fueron profundizados.
Definiciones
Polígono: Se llama polígono a la porción del plano limitada por una curva cerrada, llamada poligonal.
Polígono regular
Un polígono regular, es un polígono en el que todos los lados tienen la misma longitud y todos los ángulos interiores son de la misma medida.
Polígono regular
Un polígono regular, es un polígono en el que todos los lados tienen la misma longitud y todos los ángulos interiores son de la misma medida.
Elementos de un polígono regular
Centro
- Punto interior que equidista de cada vértice
Radio
- Es el segmento que va del centro a cada vértice.
Apotema
- Distancia del centro al punto medio de un lado.
Ángulos de un polígono regular

Ángulo central de un polígono regular
Si n es el número de lados de un polígono:
- Es el formado por dos radios consecutivos.
- Ángulo central = 360° : n
- Ángulo central del pentágono regular= 360° : 5 = 72º
Ángulo interior de un polígono regular
- Es el formado por dos lados consecutivos.
- Ángulo interior =180° − Ángulo central
- Ángulo interior del pentágono regular = 180° − 72º = 108º
Ángulo exterior de un polígono regular
- Es el formado por un lado y la prolongación de un lado consecutivo.
- Los ángulos exteriores e interiores son suplementarios, es decir, que suman 180º.
- Ángulo exterior = Ángulo central
- Ángulo exterior del pentágono regular = 72º
Polígono inscrito
Un polígono está inscrito en una circunferencia si todos sus vértices están contenidos en ella.
 Circunferencia circunscrita
Circunferencia circunscrita
- Es la que toca a cada vértice del polígono
- Su centro equidista de todos los vértices.
- Su radio es el radio del polígono.
Clasificación de los polígonos
Los polígonos se clasifican básicamente en:Polígonos regulares: Un polígono regular es aquel en el que todos sus lados tienen igual longitud, y todos sus ángulos interiores tienen la misma medida.
Polígonos irregulares: Un polígono irregular es aquel que no es regular, por lo tanto sus lados no poseen igual longitud ni sus ángulos miden lo mismo.
En este espacio nos abocaremos al estudio de los polígonos regulares.
Clasificación de los polígonos según su número de lados.
En este espacio nos abocaremos al estudio de los polígonos regulares.
Clasificación de los polígonos según su número de lados.
Clasificación de los polígonos según su número de lados | ||
Nombre | Nº de lados | Forma geométrica |
Triangulo equilátero | 3 | |
Cuadrado | 4 | |
Pentágono regular | 5 | |
Hexágono regular | 6 | |
Heptágono regular | 7 | |
Octógono regular | 8 | |
Eneágono regular | 9 | |
Decágono regular | 10 | |
Estos son algunos de los polígonos regulares ya que la cantidad de polígonos regulares es infinita y si observamos, la progresión al ir agregando lados al polígono su forma se va aproximando cada vez más al círculo.
Existen varias formas para graficar un polígono, en el siguiente vídeo te mostrare la forma de construir un polígono inscrito en una circunferencia. Así que toma lápiz, papel, tu compás tu regla y tu transportador que comenzaremos a trabajar.
Método para graficar polígonos regulares
Ejes de simetría
Que es un eje de simetría?
Eje de simetría plano es una línea imaginaria que al dividir una forma cualquiera, lo hace en dos partes simetricas. Es decir que es una línea que atraviesa una figura de tal manera que cada lado es espejo del otro.
Todos los polígonos regulares tienen tantos ejes de simetría como lados.
En el siguiente enlace encontraras una aplicación que te puede ayudar a comprender todavía mÁs sobre los ejes de simetría
Actividad ejes de simetría
Ahora veremos las formulas que nos permiten calcular el área de los polígonos regulares.
Área del triangulo.

Área del cuadrado

Ahora veremos la fórmula para calcular el área de los polígonos de más de cuatro lados, los cuales poseen la misma fórmula. es decir que esta fórmula no sirve para calcular tanto el área de un polígono de 5 lados como para calcular el área de un polígono de 20 lados.
Realiza las siguientes actividades y luego envíalas a lucerorodrigo96@gmail.com
Circunferencia y Círculo
Circunferencia y Círculo
Circunferencia
Definición: Circunferencia es el conjunto de todos los puntos del plano que equidistan de otro punto llamado centro.
Elementos notables
Radio: Es un segmento que une el centro de la circunferencia con cualquier punto de ella.
El radio se nombra con la letra “r” o bien con sus puntos extremos.
La medida del radio es constante.
Cuerda: Es el segmento que une dos puntos de la circunferencia. Las cuerdas tienen distintas medidas.
Diámetro: Es la cuerda que pasa por el centro de la circunferencia.
El diámetro es la cuerda de mayor medida.
El diámetro se nombra con la letra “d”.
El diámetro siempre es el doble del radio: d = 2r r = d/2 .

Relación entre rectas y circunferencias
Recta secante: aquella recta que toca dos puntos de la circunferencia.
Recta tangente: aquella recta que toca un solo punto de la circunferencia.
Recta exterior: aquella recta que no toca ningún punto.
 |  |  |
Secante | Tangente | Exterior |
Circunferencias concéntricas: Son aquellas que comparten el centro.

Circunferencias interiores: No comparten ningún punto, una esta dentro de la otra.

Circunferencias tangentes interiores: Comparten un punto estando una dentro de la otra.

Circunferencias secantes: aquellas que comparten dos puntos.

Circunferencias tangentes exteriores: son aquellas que comparten un solo punto, la distancia entre sus centros es la suma de sus dos radios.

Circunferencias exteriores: son aquellas en que no comparten ningún punto, la distancia entre sus centros es mayor a la suma de sus radios.

Para construir una circunferencia solo necesitamos de nuestro compás y tener en cuenta la medida del radio de la circunferencia que queremos construir. En el siguiente video veraz como construir una circunferencia. Así que toma tus útiles y manos a la obra!!
Actividad
Ahora practica lo aprendido y grafica una circunferencia de radio 5cm y otra de diámetro 8,5cm.
Longitud de la circunferencia.
Si tomamos u trozo de hilo y rodeamos un circunferencia, nos daremos cuenta que la longitud del hilo e necesario para rodearla es igual a la medida del radio de dicha circunferencia, y un poco más como lo muestra la siguiente figura.
El siguiente enlace te mostrara tan bien la relación entre la longitud de la circunferencia y su diámetro

El diámetro de la circunferencia se relaciona con la longitud de esta a través del número pi.
Es decir:
La longitud de la circunferencia es igual a pi por el diámetro.
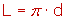
Como sabemos que la media del diámetro es igual a dos veces la medida del radio, también podemos decir que:
La longitud de una circunferencia es igual a dos pi por el radio

Círculo
Definición: El círculo es el conjunto formado por todos los puntos de una circunferencia y todos los puntos interiores de dicha circunferencia.

Construcción
Para construir un círculo procederemos de manera similar que para construir una circunferencia, pero ahora a diferencia de la circunferencia,los puntos interiores forman parte del círculo ya que el mismo es una superficie plana.
Observa el siguiente video y veras como hacerlo, así que practica la construcción.
Área del círculo.
El área del círculo es igual a pi por el radio al cuadrado


En el siguiente enlace encontraras una buena actividad que te ayudará a reforzar tus conocimientos sobre la circunferencia y el circulo Actividades
Por ultimo realiza las siguientes actividades y envíalas por correo a la siguiente dirección de correo lucerorodrigo96@gmail.com
1)La longitud de una circunferencia es 43.96 cm. ¿Cuál es el área del círculo?
2)La rueda de un camión tiene 90 cm de radio. ¿Cuánto ha recorrido el camión cuando la rueda ha dado 100 vueltas?
3)En un parque de forma circular de 700 m de radio hay situada en el centro una fuente, también de forma circular, de 5 m de radio. Calcula el área de la zona de paseo.
Poliedros regulares
Poliedros regulares
Un poco de historia: Las propiedades de estos poliedros son conocidas desde la antigüedad clásica, hay referencias a unas bolas neolíticas de piedra labrada encontradas en Escocia 1000 años antes de que Platón hiciera una descripción detallada de los mismos en Los elementos de Euclides. Se les llegó a atribuir incluso propiedades mágicas o mitológicas; Timeo de Locri, en el diálogo de Platón dice «El fuego está formado por tetraedros; el aire, de octaedros; el agua, de icosaedros; la tierra de cubos; y como aún es posible una quinta forma, Dios ha utilizado ésta, el dodecaedro pentagonal, para que sirva de límite al mundo». Los antiguos griegos estudiaron los sólidos platónicos a fondo, y fuentes (como Proclo) atribuyen a Pitágoras su descubrimiento. Otra evidencia sugiere que sólo estaba familiarizado con el tetraedro, el cubo y el dodecaedro, y que el descubrimiento del octaedro y el icosaedro pertenecen a Teeteto, un matemático griego contemporáneo de Platón. En cualquier caso, Teeteto dio la descripción matemática de los cinco poliedros y es posible que fuera el responsable de la primera demostración de que no existen otros poliedros regulares convexos.

Como vemos los poliedros regulares desde siempre han fascinado a los hombres a lo largo de la historia.
Ahora veremos cada uno de los poliedros regulares y sus características.
Definición:
Poliedro regular es aquel cuyas caras son todas polígonos regulares iguales, y todos sus diedros y ángulos poliedros también iguales.
Para que estas condiciones se cumplan, el poliedro tiene que ser convexo, puesto que en los cóncavos los ángulos diedros no son todos iguales.
Solo existen 5 poliedros regulares y ellos son:
Tetraedro:
El más sencillo de los poliedros regulares es el tetraedro que, como su nombre indica, tiene cuatro caras triangulares. Los triángulos de las caras son todos triángulos equiláteros.
Tetraedro y sus características
- 4 caras
- 4 vértices
- 6 aristas
- Tetraedro para recortar
- Modelo de tetraedro

Hexaedro(cubo): El cubo tiene seis caras cuadradas por lo cual a veces también se le llama hexaedro regular.
Hexaedro y sus características
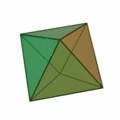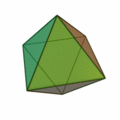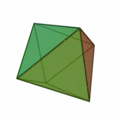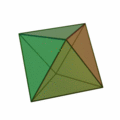
Octaedro: El octaedro tiene ocho caras triangulares.Las cuales son triángulos equiláteros.
Octaedro y sus características
- 8 caras
- 6 vértices
- 12 aristas
- Octaedro para recortar
- Modelo de octaedro
Dodecaedro: El dodecaedro tiene doce caras pentagonales.
Dodecaedro y sus características
- 12 caras
- 20 vértices
- 30 aristas
- Dodecaedro para recortar
- Modelo de dodecaedro

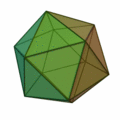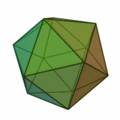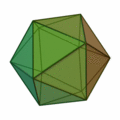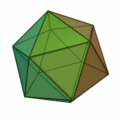
Icosaedro y sus características
- 20 caras
- 12 vértices
- 30 aristas
- Icosaedro para recortar
- Modelo de icosaedro
Por ultimo elije alguno de los cinco poliedros regulares, constrúyelo y llevalo a clase para mostrárselo a tus compañeros.
Suscribirse a:
Comentarios (Atom)