Números irracionales

REPRESENTACIÓN GRÁFICA DE LOS NÚMEROS IRRACIONALES

A cada número racional le corresponde un punto en la recta pero en realidad éstos no completan la recta, también la constituyen los irracionales. En general, representar un número con infinitas cifras decimales no periódicas es imposible y por lo tanto nos tendríamos que conformar con una aproximación. De todas  maneras, hay métodos geométricos que permiten representar algunos números irracionales en la recta numérica.

Números irracionales, son números decimales ilimitados no periódicos. El conjunto que forman se representa por la letra I

Para  representar la raíz cuadrada de un número a se siguen los siguientes pasos:

1. Descomponemos el número a como suma de dos cuadrados: a = x² + y²  (x,y enteros)
2. Dibujamos  un triángulo rectángulo de lados x, y. La hipotenusa es: 
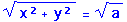
3. Para representar 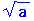 en la recta numérica se traza un arco de circunferencia de centro 0 y radio la hipotenusa 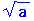, el punto de corte con la recta es la representación de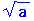 
   
   
   
   

   Por ejemplo, para calcular el punto que representa el número Ö2 realiza los siguientes pasos:

   • Levanta sobre la recta un cuadrado cuyo lado sea el segmento unidad entre el 0 y el 1. Según el teorema de Pitágoras, la diagonal del cuadrado mide Ö2.
   • Utiliza un compás para trasladar esa diagonal sobre la recta. El punto de corte del arco del compás sobre la recta representa el número Ö2.

   Fíjate en la siguiente figura y dibújala en tu cuaderno.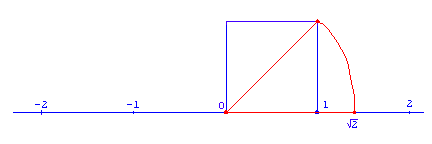

   
   
   

   
   
   
   
   
   
   El siguiente enlace te conducirá a una muy buena aplicación para practicar la representación de los números irracionales en la recta.
   Practicar la representación con Descartes 2D